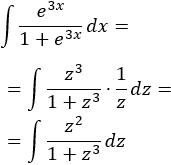Ejercicios diagrama de venn

Un diagrama de Venn utiliza círculos superpuestos u otras figuras para ilustrar las relaciones lógicas entre dos o más conjuntos de elementos. A menudo se utilizan para organizar las cosas gráficamente, resaltando cómo los elementos son similares y diferentes. Los diagramas de Venn, también llamados «diagramas de conjuntos» o «diagramas lógicos», se utilizan ampliamente en las áreas de matemáticas, estadística, lógica, enseñanza, lingüística, informática y negocios. Muchas personas los vieron por primera vez en la escuela cuando estudiaban matemáticas o lógica, ya que los diagramas de Venn pasaron a formar parte del «nuevo plan de estudios de matemáticas» en el decenio de 1960. Pueden ser diagramas simples que implican dos o tres conjuntos con algunos elementos o pueden llegar a ser muy sofisticados, por ejemplo, en presentaciones 3D, ya que utilizan seis o siete conjuntos o más.

¿Qué es un diagrama de Venn?

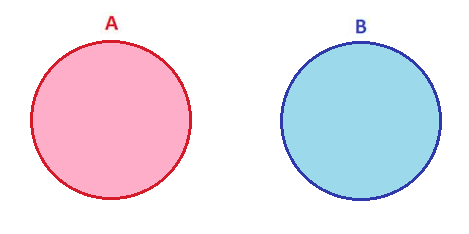
Los diagramas de Venn se utilizan para mostrar gráficamente la agrupación de elementos en conjuntos, con cada conjunto representado por un círculo u óvalo. Veremos y estudiaremos ejemplos con 2 conjuntos: el conjunto A y el conjunto B.

Estos dos conjuntos muestran 2 elementos que no pueden tener nada en común.

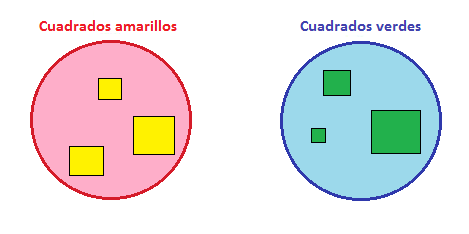
Por ejemplo, el conjunto A son cuadrados amarillos y el conjunto B son cuadrados verdes. El diagrama de Venn se vería así

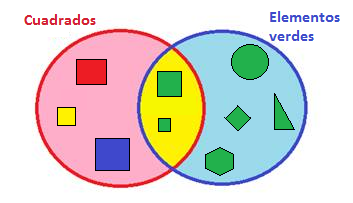
Hay otro tipo de diagrama de Venn, que son los que tienen una zona común entre los conjuntos A y B, y esta zona se llama la intersección (inter).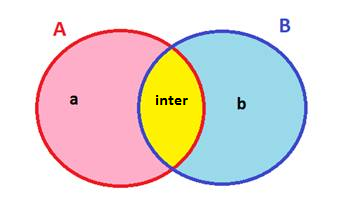Por ejemplo, el conjunto A son cuadrados y el conjunto B son figuras verdes. El diagrama quedaría de la siguiente manera:

En la zona rosa (a) están los cuadrados.
En la zona azul (b) están las figuras verdes.
En la zona amarilla (inter) están los cuadrados que son verdes.

Entrada Relacionada: Common denominator

Ejercicios diagrama de venn

De 106 personas se sabe que los que hablan solo ingles son tantos como los que hablan ingles y francés y además los que hablan solo francés es la quinta parte de los que hablan ingles. Si 10 personas no hablan ninguno de estos dos idiomas, cuántos hablan solo francés.
a) 8 b) 16 c) 24 d) 32 e) 40