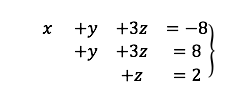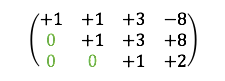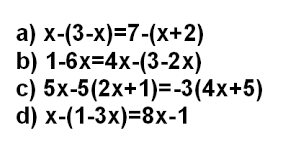Método de gauss paso a paso
Por ejemplo:
El sistema transformado en matriz:
Si lo miras, podemos eliminar directamente una de las incógnitas. Por lo tanto, este tipo de sistema es muy fácil de resolver obteniendo el valor de las incógnitas de abajo hacia arriba. De esta manera, podemos reemplazar los valores obtenidos en los anteriores.
z=2
Sustituimos el valor de "z" en la segunda ecuación y obtenemos el valor de "y":
y+3.(2)=8;
y=8-6=2
y=+2
Sustituimos el valor de "z" y "y" en la primera ecuación y obtenemos "x":
y=2
x+(2)+3.(2)=-8;
x=-16
Si nuestro sistema no es un sistema escalonado, podemos resolverlo usando el método Gaussiano. El método consiste en que "hacemos cero", es decir, sometemos las ecuaciones a transformaciones elementales:
- Multiplicamos por un número diferente de cero.
- Para sumar una ecuación a otra multiplicada por un número.
Para trabajar mejor utilizamos sólo los números (coeficientes y término independiente) y trabajamos con una estructura matricial.
Vídeos de Método de gauss paso a paso
Contenido