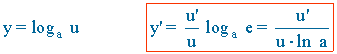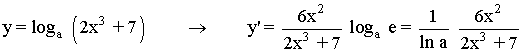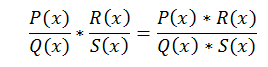Derivadas logarítmicas ejercicios resueltos paso a paso

La derivación logarítmica es una técnica de derivación que nos permite encontrar la derivada de una función aplicando las propiedades de los logaritmos. Aunque puede utilizarse para resolver muchos tipos de derivadas, es especialmente útil para funciones potenciales-exponenciales: f(x)=g(x)ϕ(x). Como ves, f(x) es una función g(x) elevada a otra función ϕ(x),. No es, por lo tanto, una función potencial, porque el exponente no es un número real constante, ni un exponencial, porque la base tampoco es constante. De ahí el nombre potencial-exponencial utilizado.

Derivada de una función exponencial y logarítmica

Una vez más, debemos hacer algunas aclaraciones. Ahora nos toca a nosotros insistir en que una función exponencial no es lo mismo que una logarítmica. En este caso, ya hemos dicho que la logaritmización es lo contrario de la potenciación. En este sentido, no es necesario hacer ciertas distinciones entre las funciones de tipo logarítmico para el potencial de las funciones de tipo logarítmico. A este respecto, hacemos las siguientes salvedades:

La función exponencial: esta función tiene el sesgo de que su argumento X se presenta siempre como un exponente. Puede expresarse de la siguiente manera: f (x) = bx. Cuando X = 1, entonces en Y = B. La forma en que esta función crece es directamente proporcional al valor de la derivada.

La función logarítmica: es una función que se expresa de la siguiente manera, f (x) = loga X. Es decir, es diferente de la función exponencial. Se caracteriza por el hecho de que su gráfica refleja la curva de la función exponencial. Es decir, son simétricas entre sí. Esto muestra que los elementos del dominio de uno de ellos son los del codominio del otro.
Una vez aclaradas las diferencias entre las dos funciones, hay que señalar que los métodos de derivación en cada una de ellas también son diferentes. En este artículo nos centramos en la descripción de los aspectos de derivación de las derivadas logarítmicas.

Entrada Relacionada: Método de Sustitución

Cómo resolver las derivadas logarítmicas

Ahora es nuestro turno de estudiar el corazón del tema propuesto en este texto. Tenemos que indicar cómo se calculan las derivadas de las funciones logarítmicas. En este caso, es necesario tener en cuenta primero ciertas propiedades de los logaritmos:

Log A + Log B = Log AB (el logaritmo de A más el logaritmo de B es igual al logaritmo del producto de A x B).
Log A - Log B = Log A/B (el logaritmo de A menos el logaritmo de B es igual al logaritmo del cociente obtenido en A ÷ B).
A Log B = Log BA (el producto de "A" por el "logaritmo de B" es igual al logaritmo de B con la potencia A).