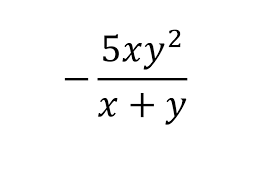Si no hay término independiente
Si no hay término independiente hay que sacar factor común. Sacar factor común de una suma (o resta) consiste en trasformarla en un producto.
Aplicaríamos la propiedad distributiva:
Ejemplo de factorización de polinomio sin termino independente
Descomponer en factores sacando factor común y hallar las raíces.
1 
La raíces son: 
y 
Sólo tiene una raíz porque que el polinomio, 
, no tiene ningún valor que lo anule. Como la x es al cuadrado, el resultado siempre será un número positivo, entonces es irreducible.
Doble extracción de factor común
Sacamos factor común de x y y.
Como 
es ahora un factor común, sacamos factor común de .
La raíces son 
y 
.
Si tenemos un binomio
Cuando tenemos un binomio, puede ocurrir alguno de los siguientes casos:
Diferencia de cuadrados
Una diferencia de cuadrados es igual a suma por diferencia.
Ejemplos de ejercicios con diferencia de cuadrados:
Descomponer en factores y hallar las raíces
Las raíces son 
y 
El ultimo termino es también una diferencia de cuadrados, entonces:
Las raíces son 
y
Suma de cubos
Ejemplo de ejercicio con suma de cubos:
