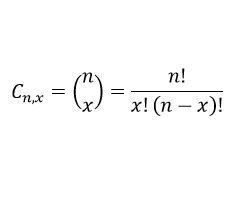Raíz cuadrada con decimales ejercicios resueltos

Método de cálculo de la raíz cuadrada

• Radical, es sólo el símbolo que indica que es una raíz cuadrada.
• Radical, es el número al que se le dará la raíz cuadrada.
• Línea de la raíz cuadrada, allí distinguirás el resultado.
• Líneas auxiliares, nos ayudarán a resolver la raíz cuadrada.
• Residuo, es el número final del proceso para resolver la raíz cuadrada.

Raíz cuadrada con decimales ejercicios resueltos

A continuación, le mostraremos paso a paso cómo resolver una raíz cuadrada a mano. Estos mismos pasos son los que encontrarás si utilizas la herramienta online que tienes al principio. Puedes leer estos pasos e intentar practicar paso a paso con la herramienta hasta que puedas resolverla por ti mismo.

• El número se separa del número residente (en el ejemplo, 5836.369) en grupos de dos dígitos. La separación se hace desde el punto decimal (si lo hay) a la derecha y a la izquierda. Si en el lado del decimal (a la derecha del punto, es decir, 369) no hay un número par de dígitos, es evidente que habría un uno suelto: en ese caso, se añadiría un cero. Si en el lado del número entero (a la izquierda del punto, es decir 5836) hay un número suelto, quedaría así. En la imagen de la derecha podemos ver el número 5836.369 dividido en grupos de dos dígitos; después del número 9 se ha añadido un cero (en azul) porque en el lado decimal no puede haber un grupo de un dígito (en el ejemplo, esta separación sería así: 58/36.36/90)
• Se busca un número que multiplicándose por sí mismo (es decir, al cuadrado) resulte en el número que coincida o se acerque más al primer grupo de números de la izquierda (en el ejemplo, 58). El resultado no puede ser mayor que 58. Una vez encontrado, el número se añade a la parte de la raíz. En este caso el número sería 7, porque 7×7 es 49. Otra posibilidad sería 6×6, pero daría 36 (que estaría más lejos que 58) y 8×8, pero daría 64 (que superaría a 58)
• El número obtenido (7) es el primer resultado de la raíz cuadrada. En el paso anterior lo escribimos en el cuadro de la derecha. Ahora lo multiplicamos por sí mismo. El resultado (49) se escribe bajo el primer grupo de cifras de la izquierda (58), y procedemos a restarlo. El resultado de la resta (58-49) es 9. Una vez obtenido el resultado de la resta, se baja el siguiente grupo de dos figuras (36), de modo que la siguiente figura de la raíz es ahora la unión del resultado de la anterior resta con las nuevas figuras bajadas (es decir, 936). Para continuar la extracción de la raíz cuadrada se multiplica por 2 el primer resultado (7) y se escribe justo debajo de él, en la siguiente línea auxiliar (en la imagen, el 14 se escribe justo debajo del 7, ya que 7×2 es 14).
• En este paso hay que encontrar un número n que, sumado a 14, y multiplicado por ese mismo n, resulta en un número igual o menor a 936. Es decir, podría ser 141×1, 142×2, 143×3... y así hasta 149×9. Muchas veces se utiliza el procedimiento para encontrar ese número, aunque se puede utilizar el método de dividir los dos primeros dígitos del residuo (93) por el número de la línea auxiliar (14). El primer dígito del resultado que no es cero, aunque sea un decimal, suele ser el que buscamos. El resultado se suma al número de la raíz y de la línea auxiliar. En este caso 93 dividido por 14 es 6. Así que la operación buscada es 146×6 = 876 (operación que sumamos en la línea auxiliar). El siguiente resultado de la raíz cuadrada es 6. También procedemos a anotarlo en la radicanda.
• El procedimiento es el mismo que el anterior. El resultado de la operación anterior (876) se coloca bajo el número que proviene de la sustracción anterior (936) y se restan. Al resultado de la sustracción (60) se le suma el siguiente grupo de cifras del radical (en este caso, 36). Si el siguiente grupo se encuentra después de la coma, se añade una coma decimal al número de la raíz. El nuevo número obtenido es 6036.
• Volvemos al procedimiento del paso 3. El número de la raíz (76) se multiplica por dos (resultando en 152). Buscamos un número que sumado a 152 y multiplicado por ese mismo número nos da una cantidad aproximada de 6036. Sería, por lo tanto, 1521×1, 1522×2, 1523×3, etc. Podemos hacerlo por ensayo y error, o por el procedimiento de dividir en este caso, los tres primeros dígitos de la raíz por los tres primeros dígitos de la línea auxiliar (nótese que antes eran los dos primeros dígitos), es decir, 603/152 (el número buscado es 3, ya que el resultado es 3,9 y hemos dicho que la cifra que debemos tomar es la primera). La operación a realizar es, por lo tanto, 1523×3. El resultado (4569) se coloca debajo del último resto y se procede a buscar la diferencia (que es 1467). Una vez realizada la sustracción, se baja el siguiente grupo de cifras y el proceso continúa. Nótese que el número a dividir entre la línea auxiliar y el residuo se incrementa.
• Se continúa el mismo proceso, la raíz se multiplica de nuevo por dos (sin tener en cuenta el punto decimal) (763 x 2 = 1526). El resultado de la multiplicación se suma a la tercera línea auxiliar, los cuatro primeros números del residuo (1467) se dividen de nuevo por el resultado de la multiplicación (1526),(nótese que son los cuatro primeros dígitos, cuando antes eran los tres primeros), lo que nos da un resultado de 0,9 (como dijimos antes, el primer número que no es cero se toma aunque sea decimal, por lo tanto, el dígito buscado es 9). El nueve se suma en la línea de la raíz y en la tercera línea auxiliar, y se multiplica el 9 por 15269, lo que nos da un resultado de 137421, esta cifra se resta de 146790 y nos da un resultado de 9369.

Raíz cuadrada con decimales ejercicios resueltos

Resolver la raíz cuadrada de: 6256