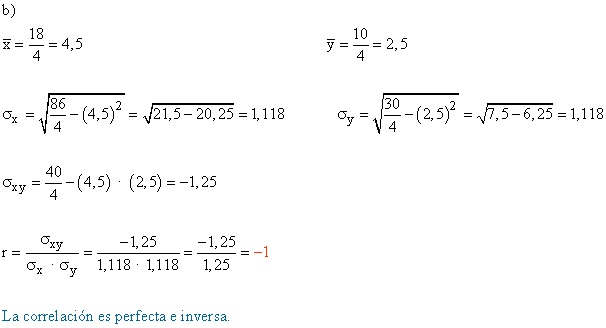Coeficiente de correlación de pearson ejercicios resueltos

El coeficiente de correlación de Pearson es una prueba que mide la relación estadística entre dos variables continuas. Si la asociación entre los elementos no es lineal, entonces el coeficiente no está adecuadamente representado. El coeficiente de correlación puede tomar un rango de valores de +1 a -1. Un valor de 0 indica que no hay asociación entre las dos variables. Un valor mayor que 0 indica una asociación positiva. Es decir, a medida que el valor de una variable aumenta, también lo hace el valor de la otra. Un valor menor que 0 indica una asociación negativa; es decir, a medida que el valor de una variable aumenta, el valor de la otra disminuye.

Coeficiente de correlación de pearson

Para llevar a cabo la correlación de Pearson, debe cumplirse lo siguiente:

La escala de medición debe ser una escala de intervalo o de proporción.
Las variables deben estar distribuidas de manera aproximada.
La asociación debe ser lineal.
No debe haber valores atípicos en los datos.

Cómo se calcula el coeficiente de correlación de Pearson

La fórmula del coeficiente de correlación de Pearson es la siguiente:

Donde:

"x" es igual a la variable número uno, "y" pertenece a la variable número dos, "zx" es la desviación estándar de la variable
uno, "zy" es la desviación estándar de la variable dos y "N" es el número de datos.

Interpretación del coeficiente de correlación de Karl Pearson

El coeficiente de correlación de Pearson tiene por objeto indicar cuánto se asocian dos variables entre sí para que

Entrada Relacionada: Problemas de sistemas de ecuaciones con dos incognitas

Correlación menor que cero: Si la correlación es menor que cero, significa que es negativa, es decir, que las variables están inversamente relacionadas.

Cuando el valor de alguna variable es alto, el valor de la otra variable es bajo. Cuanto más se acerca a -1, más clara es la covariación extrema. Si el coeficiente es igual a -1, nos referimos a una correlación negativa perfecta.

Correlación mayor que cero: Si la correlación es igual a +1, significa que es perfectamente positiva. En este caso significa que la correlación es positiva, es decir, que las variables están directamente correlacionadas.

Cuando el valor de una variable es alto, el valor de la otra también es alto, lo mismo ocurre cuando son bajas. Si está cerca de +1, el coeficiente será la covariación.

Correlación igual a cero: Cuando la correlación es igual a cero significa que no es posible determinar algún sentido de covariación. Sin embargo, no significa que no haya una relación no lineal entre las variables.

Cuando las variables son independientes significa que están correlacionadas, pero esto significa que el resultado es verdadero.

Ventajas y desventajas del coeficiente de correlación de Pearson

Entre las principales ventajas del coeficiente de correlación de Karl Pearson están

El valor es independiente de cualquier unidad utilizada para medir las variables.
Si la muestra es grande, la precisión de la estimación es más probable.

Algunas de las desventajas del coeficiente de correlación son

Es necesario que las dos variables se midan a un nivel cuantitativo continuo.
La distribución de las variables debe ser similar a la curva normal.

Entrada Relacionada: Área entre las gráficas de funciones ejercicios resueltos

Coeficiente de correlación de pearson ejercicios resueltos

En una empresa de transporte trabajan 4 conductores. Los años de antigüedad de sus permisos de conducir y el número de infracciones cometidas en el último año por cada uno de ellos son los siguientes :

X : años de antigüedad	3	4	5	6
Y : infracciones	4	3	2	1

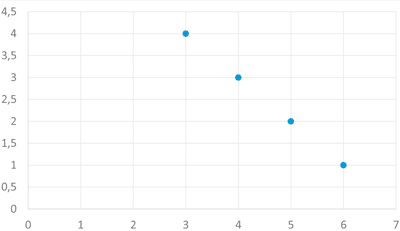
Representar gráficamente los datos anteriores. Razonar si los datos muestran una correlación positiva o negativa.
Calcular el coeficiente de correlación e interpretarlo en términos de la situación real.