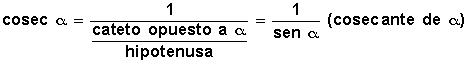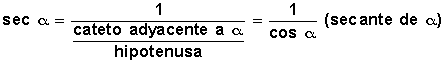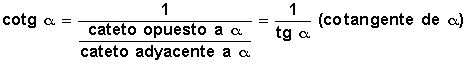
¿Cómo identificar los catetos en un triángulo rectángulo?
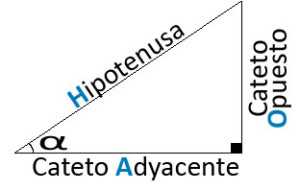
Las catetos son los dos lados del triángulo rectángulo que forman el ángulo recto.
El triángulo rectángulo tiene dos catetos. Estos se definen de acuerdo con el ángulo de referencia agudo α:
- Cateto adyacente (o contigua): lado que forma el ángulo recto y es adyacente al ángulo α.
- Cateto opuesto: lado que forma el ángulo recto y es opuesto al ángulo α.
- Cateto del triángulo recto, siendo el ángulo de referencia el superior.
Si el ángulo de referencia no fuera el ángulo α sino el ángulo β (el superior) las patas adyacentes y opuestas se invertirían.
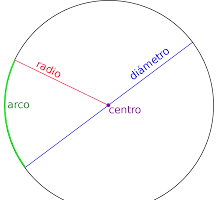
La hipotenusa es el lado más grande del triángulo opuesto al ángulo recto. Hay varios teoremas que relacionan los catetos y la hipotenusa.
Razones trigonométricas de un triángulo rectángulo
Seis son las proporciones o funciones trigonométricas que pueden establecerse para cualquiera de los dos ángulos agudos de un triángulo rectángulo; de éstas, tres son fundamentales y tres son recíprocas, como vemos acá:
Funciones trigonométricas
Fundamentales
- sen seno
- cos coseno
- tan (tg) tangente
Recíprocas
- cosec (csc) cosecante
- sec secante
- cotan (cotg) cotangente
Las razones trigonométricas con respecto a alfa (α)se definen como:
Seno
Coseno
Tangente
Cosecante
Secante
Cotangente
Contenido