¿Qué es el producto vectorial de dos vectores?
En matemáticas, el producto vectorial es una operación entre dos vectores en el espacio tridimensional (en R3). El resultado de esta operación vectorial es un vector de dirección perpendicular a los dos vectores multiplicadores, y de módulo igual al producto de los módulos de los vectores multiplicadores por el seno del ángulo que forman. Es decir, su fórmula es
Como ves en la fórmula anterior, el producto vectorial se denota con un , por eso también se llama producto cruzado. A veces también se dice producto vectorial de Gibbs, ya que fue él quien lo inventó.
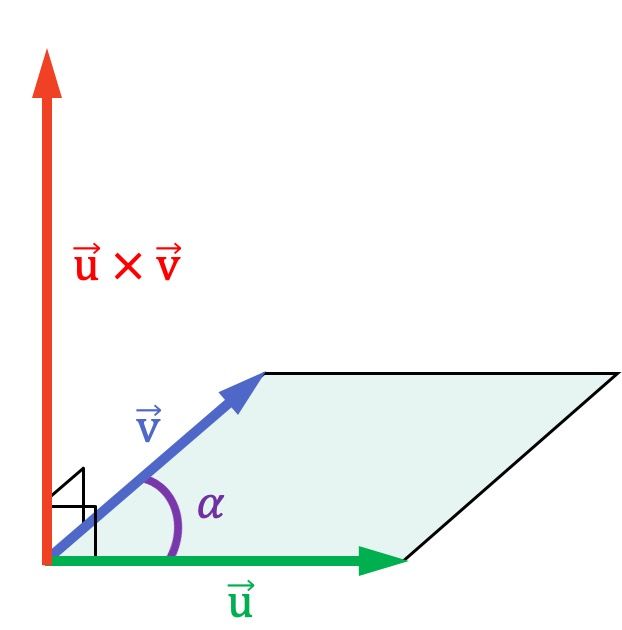
Como se puede ver en la representación gráfica anterior, el producto vectorial es perpendicular a los dos vectores que se están multiplicando y, en consecuencia, es normal al plano que los contiene.
Fórmula para calcular el producto vectorial de dos vectores
Si conocemos las coordenadas cartesianas de los vectores, la forma más fácil de calcular su producto vectorial es resolviendo un determinante 3×3. Veamos cómo se hace esto:
Sean dos vectores cualesquiera:
Su producto vectorial es:
Donde los vectores son los vectores unitarios en los sentidos de los ejes X, Y, Z respectivamente.
Veamos un ejemplo de cómo calcular el producto vectorial entre dos vectores:
Para determinar el producto vectorial entre los vectores, debemos hacer el siguiente determinante de orden 3:
En este caso, resolveremos el determinante por adjuntos o cofactores (también se podría utilizar la regla de Sarrus):
Por lo tanto, el resultado del producto vectorial de los dos vectores es:
Determinar la dirección y la dirección del producto vectorial
A veces no necesitamos conocer los componentes del producto vectorial resultante, sino que basta con encontrar su módulo, su sentido y su dirección. Esto suele ocurrir en la física, especialmente en el cálculo de las fuerzas.
Así, hay varias reglas para encontrar la dirección y el sentido del producto vectorial, las más conocidas son la regla de la mano derecha, ya sea con tres dedos o con la mano entera, y la regla del sacacorchos. Puedes usar cualquiera de ellas para no tener que conocerlas todas.
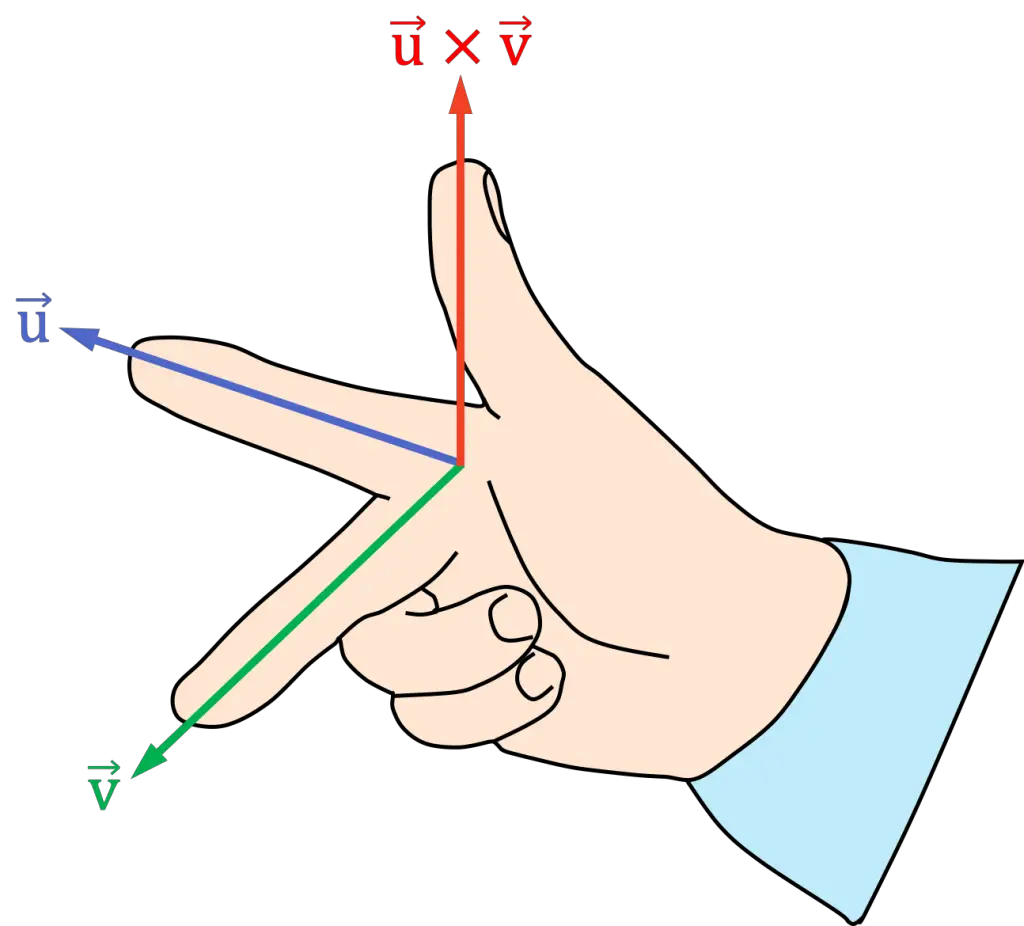
Regla de la mano derecha (3 dedos)
La versión de tres dedos de la regla o ley de la mano derecha consiste en realizar los siguientes pasos:
- Coloca el dedo índice de la mano derecha en la dirección del primer vector del producto vectorial
- Coloca el dedo medio (o corazón) de la mano derecha en la dirección del segundo vector del producto vectorial
- La posición resultante del dedo pulgar señala la dirección y el sentido del producto vectorial
Producto punto ejercicios resueltos
Calcula el producto vectorial entre los siguientes dos vectores:
Para determinar el producto vectorial entre los vectores, debemos resolver el siguiente determinante de dimensión 3×3:
En este caso, resolveremos el determinante por adjuntos o cofactores (pero también se podría utilizar la regla de Sarrus):
De manera que el resultado del producto vectorial de los dos vectores es:
Contenido