Clases de intervalos
- Intervalo abierto: El intervalo abierto es el conjunto de todos los números reales mayores que a y menores que b.
- Intervalo cerrado: Intervalo cerrado, es el conjunto de todos los números reales mayores o iguales que a y menores o iguales que b.
- Intervalo semiabierto desde la izquierda: El intervalo semiabierto desde la izquierda es el conjunto de todos los números reales mayores que a y menores o iguales que b.
- Intervalo semiabierto de la derecha es el conjunto de todos los números reales mayores o iguales que a y menores o iguales que b.
Unión e intersección de intervalos
Cuando queremos ver qué números tienen en común varios intervalos, o queremos tener un nuevo intervalo que incluya los números de varios intervalos, podemos hacer dos tipos de operaciones;
Unión de intervalos
La unión de dos intervalos A y B, que se representa A U B, es el intervalo formado por todos los elementos que están en A o que están en B.
Ejemplo:
Si tenemos los intervalos A = ] -2, 11] y B = [5, +∞[. Determinar A U B.
Si representamos los intervalos A y B;
Para representar la unión de intervalos A y B tomamos todos los números de A y B.
Entonces;
Intersección de intervalos
La intersección de dos intervalos A y B, representada por A ∩ B, es el intervalo formado por todos los elementos o números que A y B tienen en común.
Si A y B no tienen elementos en común, la intersección entre A y B es igual al conjunto vacío (ᴓ).
Ejemplo:
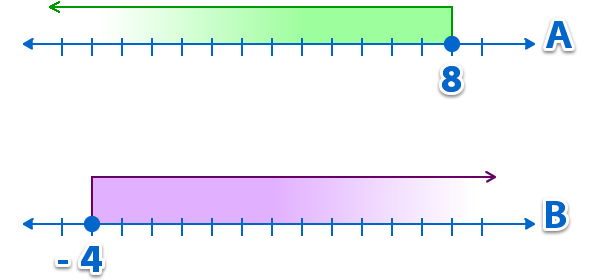
Si tenemos los intervalos A = ] -∞, 8] y B = [- 4, +∞[ Determinar A ∩ B.
Si representamos los intervalos A y B;
Contenido