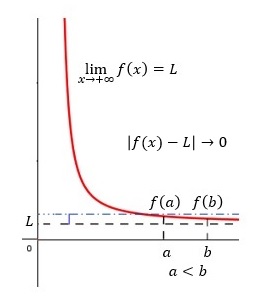
Límites que tienden a infinito
Se dice que hay un límite infinito cuando la función f(x) alcanza valores que crecen continuamente, es decir que podemos hacer la función tan grande como queramos. Se dice que f(x) se desvía al infinito. Por ello, el valor al que tiende la variable independiente x puede ser tanto a un número finito, como tender al infinito (límites al infinito).
Ejemplo de límite infinito
Indicar si existe el siguiente límite:
Si graficamos la función:
Para que exista el límite, las imágenes deben acercarse a un valor real cuando las x están cerca de cero. Sin embargo, en este problema, las imágenes no se acercan a ningún valor real. A partir del gráfico, podemos ver que cuando los valores x están cerca de cero, las imágenes crecen sin límite, por lo tanto el límite no existe.
Aunque el límite no existe, podemos usar la notación de límite para expresar el comportamiento de la función: las imágenes tienden al infinito (crecen sin límite), cuando x tiende a cero.
Esto no significa que el límite exista. Es más, ese infinito es la razón de la inexistencia del límite, porque el infinito no es un número real, y para que el límite exista, las imágenes f(x) deben acercarse a un número real.
Contenido