Integrales de raíces

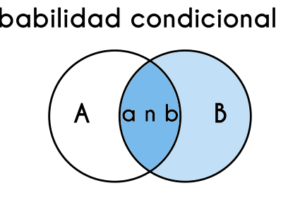
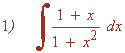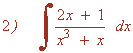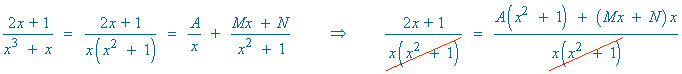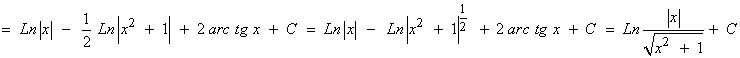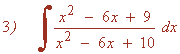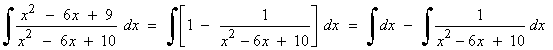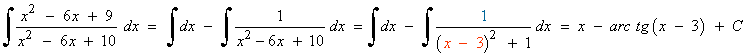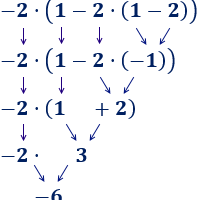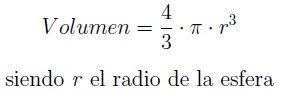Integrales de raíces

Las raices del denominador son imaginarias:      x = ± √-1 = ± i

Resolvemos la integral descomponiéndola en dos sumas:

Podemos factorizar el denominador así:

x³ + x = x(x² + 1)

Luego las raíces de   x³ + x = 0   son :     0   ,   ±√-1

Son tres raíces: una real simple y dos complejas simples.

Por tanto:

Como los denominadores son iguales, los numeradores también tienen que ser iguales:

Para   x = 0 :      1 = A

Para   x = 1 :      3 = 2A + M + N      ⇒      3 = 2 + M + N      ⇒      M + N = 1

Para   x = -1 :      -1 = 2A + M - N      ⇒      -1 = 2 + M - N      ⇒      M - N = -3

Resolviendo el sistema se tiene:      M = - 1   ,   N = 2

Resolviendo las integrales inmediatas y aplicando las propiedades de los logaritmos:

Como numerador y denominador tienen mismo grado, realizamos la división y aplicamos la fórmula del cociente:

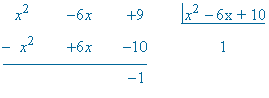
La primera integral es inmediata. La segunda es de tipo racional, por lo que calculamos las raíces del denominador y después lo factorizamos: