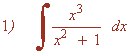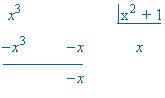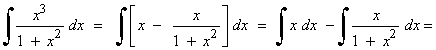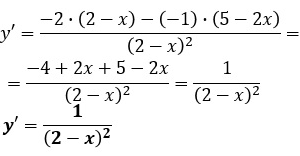Integrales con raíz en el denominador

Aparte de la fuerza bruta de la computación numérica, aquellos que buscan resolver integrales tienen sólo unas pocas técnicas basadas en el cálculo con las que trabajar. A menudo es el repertorio de herramientas matemáticas como el álgebra, la trigonometría y otros trucos no matemáticos lo que permite que muchas de las integrales más difíciles se resuelvan sin la ayuda de una computadora.

Integrales con raíz en el denominador

Reescribir las raíces cuadradas como exponentes de un medio. Tomar la raíz cuadrada de un término es lo mismo que elevar el mismo término a la potencia de un medio.

Combinar la parte superior e inferior de la fracción que está debajo del mismo exponente de un medio como un posible paso siguiente. Es posible que la integral pueda entonces ser resuelta usando la regla de poder. Sin embargo, también es posible que esto sólo complique más la situación y deba evitarse.

Sustituir todos o parte de los términos bajo el símbolo de la raíz cuadrada. Esto funciona mejor cuando hay un polinomio, como una ecuación cuadrática, debajo de la raíz cuadrada. Recuerde que debe sustituir la expresión diferencial por la derivada de la variable de sustitución.

Utilice una sustitución trigonométrica. Si ninguna de las dos estrategias anteriores convierte el integrando en una forma que pueda ser fácilmente integrada, establezca varias funciones trigonométricas para que coincidan con toda o parte de la expresión bajo la raíz cuadrada y sustituya.