Cómo resolver sistemas de inecuaciones con dos incógnitas
- Resolver la inecuación:
- Transformamos la desigualdad en igualdad.
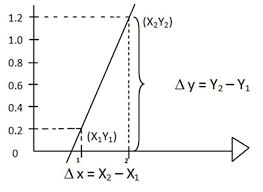
- Damos a una de las dos variables dos valores, con lo que obtenemos dos puntos.
- Al representar y unir estos puntos obtenemos una recta.
- Tomamos un punto, por ejemplo el
, los sustituimos en la desigualdad. Si se cumple, la solución es el semiplano donde se encuentra el punto, si no la solución será el otro semiplano.
Casos posibles de inecuaciones
- Menor o igual
Tomamos el punto y lo sustituimos en la inecuación.
Como se cumple la desigualdad la solución es el semiplano donde se encuentra , incluyendo la recta porque tomamos los puntos menores y también los iguales
En este caso dibujamos la recta con trazo continuo
- Menor
Tomamos el punto y lo sustituimos en la inecuación.
Como se cumple la desigualdad la solución es el semiplano donde se encuentra
En este caso (menor que, pero no igual) los puntos de la recta no pertenecen a la solución
En este caso dibujamos la recta con trazo discontinuo
- Mayor
Tomamos el punto y lo sustituimos en la inecuación.
No
Como no se cumple la desigualdad, la solución es el semiplano donde no se encuentra
En este caso (mayor que, pero no igual) los puntos de la recta no pertenecen a la solución.
En este caso dibujamos la recta con trazo discontinuo
- Mayor o igual
Tomamos el punto y lo sustituimos en la inecuación.
No
Como no se cumple la desigualdad, la solución es el semiplano donde no se encuentra
En este caso (mayor o igual) los puntos de la recta pertenecen a la solución.
En este caso dibujamos la recta con trazo continuo
Contenido
