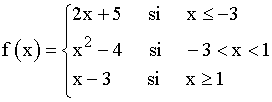Funciones a trozos
Las funciones por ramas son muy importantes para modelar el comportamiento de los fenómenos reales de su día a día.
Su compañía telefónica fija el precio de una llamada con un coste de establecimiento de 1 Además, los primeros 5 minutos de la llamada se pagan a 0,5 euros. Después de eso, el costo del minuto es de 0,7 euros.
A partir de esta situación podemos encontrar una función f(x) que nos permite saber la cantidad de una llamada a partir de los minutos x que dura. Está claro que el valor de x debe ser mayor que 0, para que pueda existir una llamada, y por lo tanto se nos cobra por ella.
Funciones a trozos ejemplos
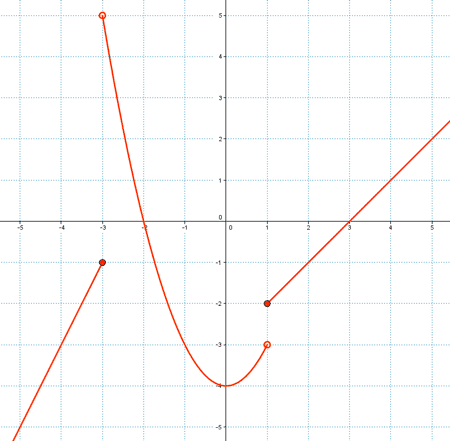
Representa la gráfica de la siguiente función :
Representamos la gráfica correspondiente a cada uno de los intervalos.
x ≤ - 3 → f ( x ) = 2x + 5
| x | - 5 | - 4 | - 3 |
|---|---|---|---|
| y = f ( x ) | - 5 | - 3 | - 1 |
- 3 < x < 1 → f ( x ) = x 2 - 4
| x | - 2 | - 1 | 0 |
|---|---|---|---|
| y = f ( x) | 0 | - 3 | - 4 |
x ≥ 1 → f ( x ) = x - 3
| x | 1 | 2 | 3 |
|---|---|---|---|
| y = f ( x ) | - 2 | - 1 | 0 |
Por último, representamos gráficamente las gráficas de cada uno de los intervalos :
Contenido