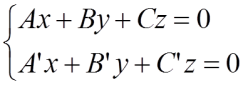Ecuación de la recta en el espacio
Para determinar una línea en el espacio necesitamos un punto y una dirección. Cualquier vector que tenga la misma dirección que una línea dada es un vector direccional de esa línea. Es notable que, como en el plano, dados dos puntos podemos obtener un punto y un vector y viceversa.
Ecuación de la recta en el espacio
Para definir una recta necesito un punto y un vector.
Si el punto fuese p y el vector v=(a,b,c) , la recta contiene al vector y su ecuación sería:
ECUACIÓN PARAMÉTRICA: despejamos las variables:
En el origen
En un punto P
ECUACIÓN CONTINUA: despejamos el parámetro:
En el origen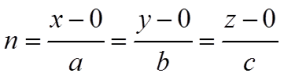
ECUACIÓN REDUCIDA: Igualamos de dos en dos la forma continua y obtenemos dos
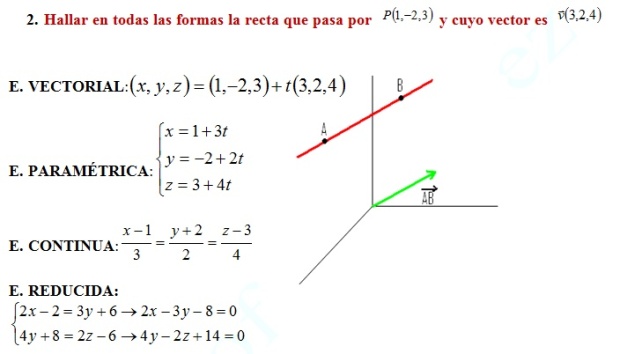
Ejemplos de Ecuación de la recta en el espacio
Contenido