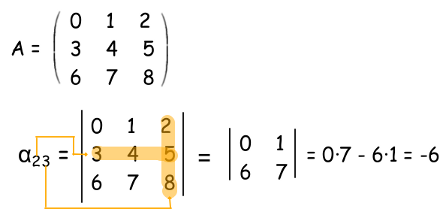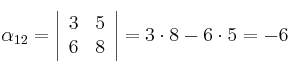Matriz complementaria
En una matriz cuadrada A llamamos menor complementario del elemento , y lo representamos por
al determinante de la matriz resultante de eliminar la fila i y la columna j de la matriz A.
«Ejemplo»: Queremos calcular el menor complementario . Para ello debemos eliminar la fila 2 y la columna 3, y calcular el determinante de la submatriz resultante.
En la misma matriz calculamos ahora los menores complementarios a11 y a12
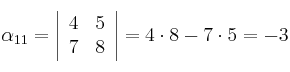
Matriz adjunta
Se llama adjunto del elemento aij a su menor complementario anteponiendo:
El signo es + si i + j es par.
El signo es − si i + j es impar.

El valor de un determinante es igual a la suma de productos de los elementos de una fila (o una columna) por sus adjuntos correspondientes:


Contenido