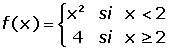Definición
Función de una variable real: Una función f de ℝ en ℝ es continua en el punto a de ℝ si hay un límite de f(x) cuando x almacena a y ese límite coincide con f(a). Si no, la función es discontinua en el punto a.
La función anterior es continua en su dominio (ℝ) si es continua en todos los puntos de ℝ.
Ejemplos
- Las funciones polinómicas son continuas en ℝ.
- Las funciones racionales son continuas a lo largo de ℝ, excepto en los puntos en los que el denominador está anulado. Por ejemplo, f(x) = 1 / (x -1) es continua en todos los reales excepto en x = 1.
- Las funciones constantes son continuas a lo largo de ℝ. Por ejemplo, f(x) = 3.
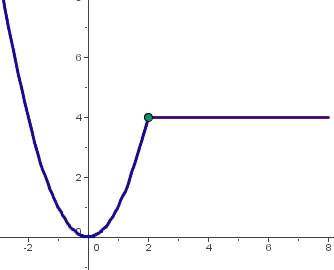
- La función definida por partes,
es continua para los puntos x < 2 porque es polinómica y para los puntos x > 2 porque es constante. Además, la función es continua en el punto x = 2, porque los límites laterales de f(x) cuando x tiende a 2 coinciden y son iguales a f(2). Su gráfica es:
Continuidad lateral
- Una función f(x) se deja continua en el punto x = a si el límite de f(x) existe cuando x tiende a la izquierda y es igual a f(a).
- Una función f(x) es derecha-continua en el punto x = a si el límite de f(x) existe cuando x tiende a la derecha y es igual a f(a).
- Si la función f(x) es continua a la derecha y a la izquierda de a, entonces es continua en a.
Tipos de discontinuidades
Las discontinuidades se clasifican como evitables e inevitables. Si la función f(x) no es continua en el punto x = a, entonces la discontinuidad es:
- Evitable: si f(a) no está definido pero el límite de f(x) existe cuando x tiende a a. O bien, existe el límite de f(x) cuando x tiende a a pero no coincide con f(a).
- No evitable o esencial: si los límites laterales no coinciden (primera especie esencial) o no existe uno de ellos (segunda especie esencial).
Contenido