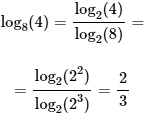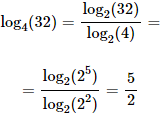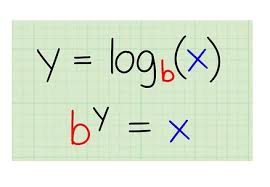
Qué es un logaritmo
El logaritmo es el exponente de una potencia con una base determinada, el logaritmo de un número debe ser positivo, es decir, el argumento y la base de un logaritmo corresponden a números reales (números positivos).
Los logaritmos nos permiten convertir el producto en una suma (la primera de las propiedades de los logaritmos que hemos revisado, es más fácil sumar que multiplicar), el cociente en una resta (es más fácil restar que dividir), una potencia en una multiplicación y una raíz en una simple división.
Simbología del logaritmo
El logaritmo está representado por la abreviatura:
log
Partes del logaritmo
El logaritmo consiste en 3 partes fundamentales:
logb a = c
- La letra "a": Es el argumento.
- La letra "b": Es la base del logaritmo.
- La letra "c": Es el logaritmo o resultado del logaritmo.
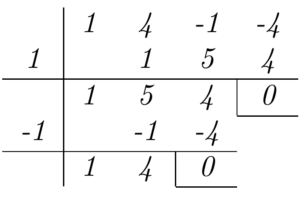
Ejemplos de cómo resolver logaritmos
Qué es un logaritmo neperiano
El logaritmo natural se conoce generalmente como el logaritmo nepalés, aunque son conceptos esencialmente diferentes.
En matemáticas, el logaritmo natural o logaritmo nepalés se denomina logaritmo cuya base es el número e, un número irracional cuyo valor aproximado es 2,7182818284590452353602874713527. El logaritmo natural se anota como ln(x), como loge(x) y en algunos contextos como log(x), porque para ese número se cumple la propiedad de que el logaritmo vale 1.
Contenido