Magnitudes escalares y vectoriales
En la definición de las mediciones físicas se utilizan dos tipos de magnitudes:
- Magnitudes escalares, que están completamente definidas por un número, como la temperatura, el tiempo y la densidad.
- Magnitudes vectoriales, para las que se requiere un valor numérico, una dirección y un sentido de aplicación, como la velocidad, la aceleración o la fuerza.
Las magnitudes vectoriales son especificadas por entidades matemáticas llamadas vectores, que se caracterizan por tres propiedades:
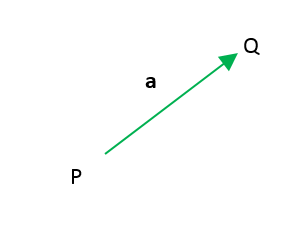
- Módulo, una cantidad numérica siempre positiva que expresa la intensidad de la magnitud. Para el vector , su módulo se expresa || o simplemente a.
- Dirección, o recta que contiene el segmento que mide la magnitud del vector.
- Sentido, u orientación de la magnitud dentro del segmento de dirección.
Suma y diferencia del vector
Cuando se opera con magnitudes vectoriales, deben cumplirse los principios del álgebra vectorial. La operación más sencilla que se hace con los vectores es la suma, que produce un nuevo vector construido, de modo que
El origen del segundo vector se sitúa sobre el final del primero.
En la posición anterior, la suma de los vectores se obtiene de manera que su origen coincide con el del primero y su final con el final del segundo vector sumado.
Suma de dos vectores. a) El segundo vector se toma sobre el extremo del primero. (b) A continuación, se dibuja el vector de la suma
Otras dos operaciones sencillas del álgebra vectorial son las siguientes:
- La diferencia entre vectores, que se obtiene como la suma del primer vector y el opuesto al segundo (aquel vector que tiene el mismo módulo y dirección que este último pero en dirección opuesta).
- El producto de un escalar (un número) por un vector produce un nuevo vector con la misma dirección y sentido que el original, módulo igual al del vector multiplicado por el número y sentido idénticos cuando el escalar es positivo y opuesto si es negativo.
Contenido