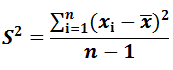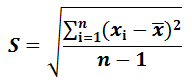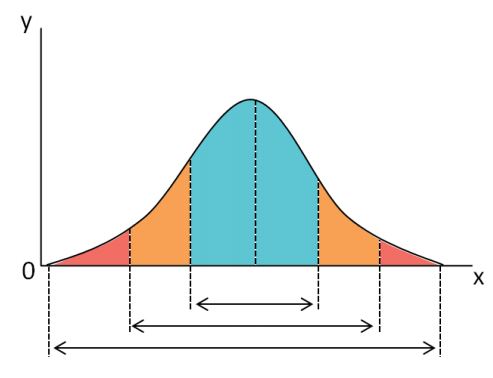
Principales medidas de dispersión
Las medidas de dispersión más conocidas son: rango, varianza, desviación estándar y coeficiente de variación (que no debe confundirse con el coeficiente de determinación). A continuación veremos estas cuatro medidas.
Rango
El rango es un valor numérico que indica la diferencia entre el valor máximo y mínimo de una población o muestra estadística. Su fórmula es:
R = Maxx - Minx
Varianza
X → Variable sobre la que se calculará la varianza
xi → Observación número i de la variable X. i puede tomar valores entre 1 y n.
N → Número de observaciones.
x̄ → Es la media de la variable X.
Desviación estándar
La desviación típica es otra medida que proporciona información sobre la dispersión con respecto al promedio. Su cálculo es exactamente igual al de la varianza, pero con la raíz cuadrada de su resultado. Es decir, la desviación estándar es la raíz cuadrada de la varianza.
Coeficiente de variación
Su cálculo se obtiene dividiendo la desviación típica por el valor absoluto del promedio del conjunto y suele expresarse en porcentaje para una mejor comprensión.
Ejemplos de medidas de dispersión
- R = DM - Dm
R = 92.4 – 75.9
R = 16.5
Determinar la varianza de los siguientes datos que representan la cantidad de glucosa en miligramos encontrada en las muestras de sangre de algunos pacientes: 14.2, 12.1, 15.6, 18.1, 14.3.
x̅ = (14.2 + 12.1 + 15.6 + 18.1 + 14.3) / 5 = 14.86
x̅ = 14.86
S2 = (14.2-14.86)2 + (12.1-14.86)2 + (15.6-14.86)2 + (18.1-14.86)2 + (14.3-14.86)2 / (5-1)
S2 = (0.4356 + 7.6176 + 0.5476 + 10.4976 + 0.3136) / 4 = 19.412 / 4
S2 = 4.853
La desviación estándar del problema anterior, de la cual tenemos una variación de 4.853, sería:
S = √4.853 = 2.2029
S = 2.2029
Contenido