Qué es la razón de dos segmentos
La relación entre dos segmentos, AB y CD, es el cociente entre la longitud del segmento AB y la longitud del segmento CD.
Está escrito:
Para calcular la razón de dos segmentos, simplemente mida sus longitudes y divídalas.
Proporcionalidad entre pares de segmentos
Llamamos proporcionalidad del segmento a la aplicación existente entre el conjunto de cantidades de longitud en sí, de manera que la aplicación es biectiva, conserva el orden, el mismo y también mantiene la correspondencia con la operación de la suma.
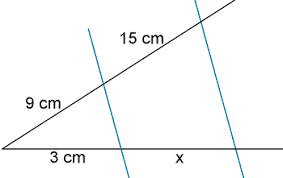
Teorema fundamental de la proporcionalidad: Dadas dos líneas r y s que se cortan en el punto O y dadas dos longitudes a y b en cada una de las líneas respectivamente de tal manera que determinan los segmentos OA=a y OB=b, como podemos ver en la imagen. Dibujando la línea que conecta los puntos A y B y trazando una línea paralela a ella que corta las líneas r y s en el punto X y X' respectivamente, entonces el segmento OX se hace corresponder con el segmento OX'.
Por lo tanto, se cumple la siguiente relación de proporcionalidad.
El teorema de Tales
Es la división de un segmento en partes iguales y también en partes proporcionales a números dados.
¿Para qué sirve el teorema de Tales?
Las aplicaciones del teorema de Tales son muchas y muy importantes: la división de un segmento en partes proporcionales, la división de un segmento en partes iguales, la cuarta y tercera proporcionales de dos segmentos dados, la media proporcional, la segmentación áurea, la cuarta proporcional de tres segmentos dados, el cálculo gráfico de productos y proporciones de segmentos dados, el cálculo de proporciones simples, proporciones armónicas dobles y cuádruples, la similitud y el estudio de escalas. Todas estas construcciones son de gran interés para la resolución de problemas y para el estudio de las transformaciones.
Cómo dividir un segmento en partes iguales con el teorema de Tales
Primer teorema de Tales
Se han identificado varias aplicaciones del primer teorema de Tales. Es necesario que a través de él un segmento pueda ser dividido en partes proporcionales. Para ello es necesario dibujar una línea L partiendo del punto A de la línea AB, y formando un ángulo. En la línea L se harán n divisiones de igual medida, y el último punto se llamará C, que se unirá con el extremo B. A través de las divisiones ya hechas, se dibujarán líneas paralelas a la unión BC.
Otra aplicación está destinada a la construcción de la cuarta proporcional geométrica de tres segmentos dados, que se llamarán a, b y c. Para ello se dibujarán dos líneas partiendo del mismo punto, formando cualquier ángulo. En una de las líneas se colocarán los dos primeros segmentos, marcando los puntos A y B; mientras que en la segunda línea se colocará el segmento c, marcando el punto C. Se dibujará una línea para unir A con C, y luego una línea paralela a ésta, creando el punto D. Es aquí donde en la segunda línea que contiene C, se origina el segmento CD, que será reconocido como la cuarta proporcional.
Segundo teorema de Tales
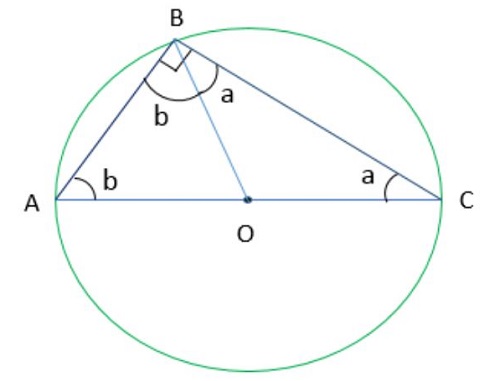
Este postulado se clasifica dentro de la categoría de los teoremas geométricos. Se centra en el estudio de un triángulo rectángulo de ángulos inscrito en un círculo, definiendo así que los vértices de la figura triangular están situados sobre el contorno del círculo, concluyendo que la primera figura está contenida dentro de la segunda.
La declaración de Tales de Mileto declara que teniendo una circunferencia central es O, y cuyo diámetro es un segmento AC, la presencia de un punto B diferente de A y C en la figura circular da lugar a un triángulo rectángulo ABC, que tiene un ángulo recto definido como <ABC.
Si se dibuja una línea desde O a cualquiera de los puntos, se obtienen los segmentos OA, OB y OC. Todos corresponden al radio del círculo, lo que determina que tengan las mismas medidas. Pero cuando estudias el segmento OB, puedes detallar que el triángulo rectángulo se divide en dos triángulos isósceles, reconocidos como OAB y OCB. También se establece que los ángulos de OAB y OBA tienen el mismo valor, así como los de OCB y OBC, identificándose a y b respectivamente. Y recordando que la suma de todos los ángulos de un triángulo es igual a 180º, se obtiene que: 2a+2b = 180º. Y el teorema puede ser finalmente verificado a través de la siguiente fórmula:
Dentro del teorema, se aplican dos premisas que permiten la solución de los problemas de los triángulos rectos y los círculos:
- La longitud de la mediana correspondiente a la hipotenusa, conocida como OB, equivale a la mitad de su valor.
- Independientemente de la posición en que se encuentre, el valor será siempre constante.
- La construcción de círculos circunscritos es posible a través de un triángulo rectángulo. Se sabe que el diámetro es igual a la hipotenusa, por lo que el radio es la mitad de su valor, que a su vez se convierte en el centro del círculo.
Ejercicios resueltos del teorema de Tales
Ejemplo:
Divide el segmento AB en 3 partes iguales.
Dibuja una semirrecta de origen en el extremo A del segmento.
Tomando cualquier medida como unidad, 3 unidades de medida de A se indican en el rayo.
Para cada división de la media pista, se dibujan líneas rectas paralelas al segmento que une B con la última división de la media pista. Los puntos obtenidos en el segmento AB determinan las 3 partes iguales en que se divide.
Para cada una de las divisiones de la media pista, se dibujan líneas rectas paralelas al segmento que une B con la última división de la media pista. Los puntos obtenidos en el segmento AB determinan las 3 partes iguales en las que se divide.
Contenido