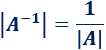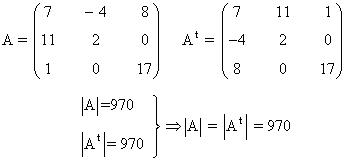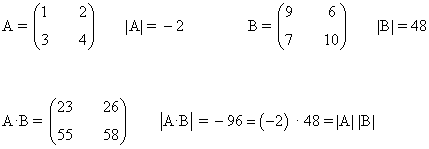Ejercicios de determinantes

El determinante de una matriz cuadrada es un número obtenido de los elementos de la matriz. Su estudio se justifica porque simplifica la resolución de los sistemas lineales y el cálculo de la matriz inversa, entre otras aplicaciones.

Propiedades de los determinantes

El determinante del producto de matrices es el producto de sus determinantes:

El determinante de una matriz con alguna fila o columna de ceros es 0.
Se puede extraer el factor común de una fila o columna multiplicando el determinante por el factor.
El mismo factor común puede extraerse de n filas o columnas multiplicando el determinante por el factor elevado a n.
Si se cambia el orden de una fila o columna, el determinante cambia de signo.
Si se cambia el orden de n filas o columnas, el determinante cambia de signo si n es impar.
Si una matriz es invertible, el determinante inverso es el inverso del determinante:

El determinante de una matriz es igual al de su traspuesta:

Si una matriz tiene filas o columnas linealmente dependientes, entonces su determinante es 0.
El determinante no cambia si se suman filas (o columnas) multiplicadas por números distintos de 0.
El determinante de una matriz diagonal es el producto de los elementos de su diagonal.