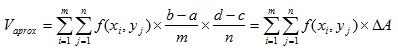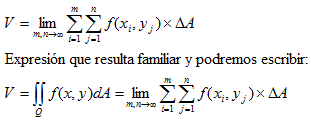Integrales dobles
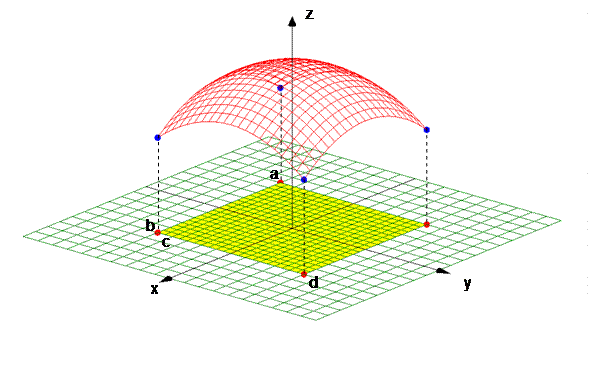
Ahora queremos integrar una función de dos variables. Con las funciones de una sola variable, integramos en un intervalo [a,b] (del dominio R de la variable independiente). Tiene sentido entonces que al integrar una función de dos variables lo hagamos en una región de R2, donde se define la función f(x,y). Empezaremos asumiendo que esta región es un rectángulo que llamaremos Q=[a,b] × [c,d], lo que significa que los dominios de x y y son a<x<b y c<y<d. Para facilitar el análisis, supongamos que f(x,y)³0, aunque esto realmente no es relevante. Veamos la gráfica de una función tal en el espacio 3D.
Si dividimos el área del rectángulo Q=[a,b]×[c,d] en pequeños rectángulos (con lados que son subintervalos de [a,b] y [c,d]) y asignamos a f(x,y) en cada uno de esos rectángulos, el valor que tiene en el punto medio, obtendremos una aproximación al volumen bajo la gráfica de f(x,y), como se observa en la siguiente figura.
Este volumen aproximado lo podremos expresar como:
Siendo evidente que tenemos una doble suma, pues tenemos que sumar estos pequeños volúmenes en ambas direcciones.
Si vamos tomando valores de m y n cada vez mayores, en el límite cuando estos números tiendan a infinito tendremos que:
La expresión a la que llegamos nos dice que el volumen bajo la función f(x,y) y por encima del plano xy viene dado por la doble integral de la función en el área del rectángulo Q=[a,b]×[c,d], lo que equivale al Teorema Fundamental de Cálculo para las integrales de una variable.
Obsérvese que en este caso el diferencial es dA y no dxdy y que no ponemos límites de integración sino que bajo la doble integral escribimos que integramos en R2 para indicar la región del plano xy en la que integramos.
Volumen integrales dobles ejercicios resueltos
Contenido