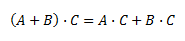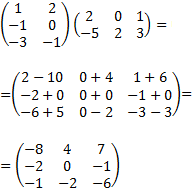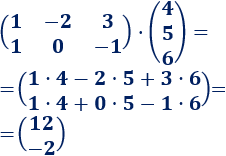
Multiplicación de matrices

La multiplicación de dos matrices consiste en unificar las matrices en una sola matriz multiplicando y sumando los elementos de las filas y columnas de las matrices de origen teniendo en cuenta el orden de los factores.

Producto de la matriz

El producto de la matriz es quizás la operación más complicada de realizar, al menos, las primeras veces. Primero vamos a explicarlo de una manera simple.

Supongamos que las matrices A y B tienen una dimensión de 2×2. El resultado del producto de la matriz A y la matriz B es la matriz de dimensión 2×2 que denotamos por AB y sus elementos son:

El elemento de la posición (1,1) de la matriz AB es el producto de la fila 1 de A y la columna 1 de B.
El elemento de la posición (1,2) de la matriz AB es el producto de la fila 1 de A y la columna 2 de B.
El elemento de la posición (2,1) de la matriz AB es el producto de la fila 2 de A y la columna 1 de B.
El elemento de la posición (2,2) de la matriz AB es el producto de la fila 2 de A y la columna 2 de B.

Hemos dicho producto de una fila por una matriz. Este producto es sólo el producto escalar de dos vectores: vector fila por vector columna. Por ejemplo, el producto de la fila (1,2,3) y (4,5,6) es 1-4 + 2-5 + 3-6 = 32.

Propiedades de las matrices

La propiedad más notable del producto de la matriz es que no es conmutativo. Es decir, el producto A-B no tiene que coincidir con el producto B-A. De hecho, si las matrices no son cuadradas, uno de los dos productos no puede ser calculado.

Entrada Relacionada: Regla de 3 compuesta

Otras propiedades:

Es asociativo

Es distributivo (a la derecha) con respecto a la suma

Es distributivo (a la izquierda) con respecto a la suma

El producto de la matriz tiene un elemento neutro y es la matriz de identidad con la dimensión adecuada para poder calcular el producto. Es decir, si la matriz A es de dimensión mxn, entonces:

A-In = A = Im-A