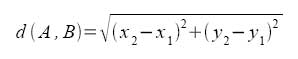Integrales con radicales
Las funciones irracionales de las integrales son simplemente funciones que se encierran en un radical.
Normalmente se conoce como integrales con raíces pero más comúnmente como integrales con radicales. Donde g(x) puede ser una función polinómica o racional.
De esta expresión podemos deducir algunas cosas con sólo probar el radical n.
Si el índice del radical n es impar, significa que podemos calcular la raíz cuadrada de cualquier número real siempre que g(x) sea también un número real.
Sin embargo, si el índice del radical es un número par, para hacer cualquier cálculo es necesario que g(x) sea positivo o cero, ya que las raíces pares de un número negativo son números imaginarios.
Cómo resolver integrales irracionales integrales con radicales ejercicios resueltos
Reescribimos el radical como potencia y hacemos ![]() y
y ![]()

![]()
Aplicamos un cambio de variable e integramos
![]()
![]()

Aplicamos ![]() y
y  e integramos
e integramos

Contenido