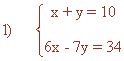Problemas de sistemas de ecuaciones con dos incognitas

Sistemas de ecuaciones con dos incognitas

• Método de sustitución. Este método consiste en aislar una de las incógnitas en una de las dos ecuaciones y sustituir su valor en la otra ecuación. Una vez resuelta esta última, la otra ecuación se resuelve sustituyendo la incógnita por este valor.
• Método de la ecuación. Este método consiste en aislar la misma incógnita de ambas ecuaciones y ecualizar los resultados obtenidos. Una vez resuelta esta última ecuación, se puede sustituir el valor de la desconocida en una de las ecuaciones iniciales y resolver la ecuación resultante para encontrar el otro valor.
• Método de reducción. Este método consiste en multiplicar convenientemente ambas ecuaciones para que, una vez restada, desaparezca una de las desconocidas y se pueda resolver la ecuación resultante. Una vez resuelta esta última ecuación, se puede sustituir el valor de la desconocida en una de las ecuaciones iniciales y resolver la ecuación resultante para encontrar el otro valor.

Hay que recordar que los pasos de cada uno de estos métodos son correctos porque transforman las ecuaciones del sistema en ecuaciones equivalentes: al sumar o restar una combinación de ecuaciones del mismo sistema, la ecuación resultante tendrá también la misma solución que las anteriores, ya que la solución es compartida por todas las ecuaciones del sistema.

Método de sustitución

Al igual que con la comida podemos elegir la bebida que la acompañe, los sistemas de ecuaciones tienen diferentes maneras o métodos de ser resueltos y depende de ti elegir el que te parezca más fácil, con el que te sientas más seguro, etc. y no tendrás ningún problema ya que las respuestas serán siempre las mismas.

Un ejemplo de esto es resolver el primer sistema de ecuaciones anterior utilizando el método de sustitución, como se puede ver en la imagen de la izquierda.

El método de sustitución consiste en el procedimiento de borrar una variable (letra) de una de las 2 ecuaciones y sustituir el resultado en la segunda ecuación (la que no elegimos primero), de esta forma los pasos a seguir (que podéis ver con detalle en la imagen) serían los siguientes:

• Borrar una incógnita en una sola de las ecuaciones (elegir la que sea más fácil de borrar).
• Una vez hecho el clearing se procede a abrir paréntesis en la segunda ecuación en los lugares donde se encuentre la letra que hemos borrado en el punto 1.
• Dentro de los paréntesis, colocamos el resultado del despeje del punto 1.
• Resolvemos la ecuación de primer grado que se ha creado para obtener el valor de la segunda desconocida.
• Con el valor del paso 4 volvemos a donde teníamos el claro en el punto 2 y colocamos ese valor (paso 4) para encontrar la primera ecuación.
• Lo comprobamos sustituyendo los valores al mismo tiempo en una de las ecuaciones originales.

Como se puede ver en la imagen, el resultado del sistema de ecuaciones es y=10 y x=35, que es exactamente el mismo resultado que el método de suma y resta, por lo que se demuestra que, independientemente del método que se elija, siempre se obtendrá el mismo resultado. Esta característica puede ayudarte a averiguar si has calculado mal en algún otro método porque debería darte el mismo resultado.

Problemas de sistemas de ecuaciones con dos incognitas