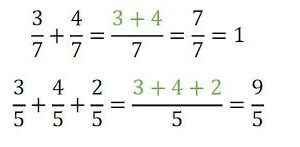
Para que sirven las fracciones
Las fracciones son expresiones matemáticas que tienen múltiples usos en la vida cotidiana, ya que sus elementos (numerador y denominador) representan conjuntos, subconjuntos o integridades que deben ser divididos o estudiados por separado. En este sentido, los principales beneficios del estudio y aplicación de las fracciones se dirigen a estos usos:
Distribución equitativa
Las fracciones permiten una distribución equitativa de un objeto dado, entre un número limitado de personas, animales o cosas; en este sentido, este beneficio de las fracciones es evidente en la vida cotidiana, cuando se distribuye una pizza, un pastel, un caramelo o cualquier otra cosa.
Para ello, las fracciones responden a la pregunta: cuántas corresponden a cada una, independientemente del objeto en cuestión a distribuir, el numerador representa el número de objetos a distribuir, mientras que el denominador corresponde al número de personas entre las que debe distribuirse el objeto.
Dividir o separar una totalidad
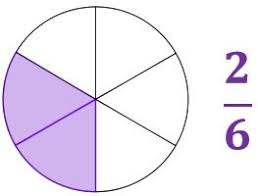
Otro uso de las fracciones es la división o separación de un todo, con la que conocemos las partes iguales en las que se clasifica un todo, o un conjunto de objetos iguales. En este sentido, las fracciones nos permiten determinar el número de partes iguales en las que se subdivide un todo.
Para ello, el denominador (número en la parte inferior de la fracción) indica el número de partes en que se divide el todo, mientras que el numerador (número superior) representa las partes de ese todo que se toman en consideración.
Representar una relación
Por último, las fracciones permiten determinar e interpretar la relación entre dos números; en este caso, la relación puede venir dada por dos conjuntos diferentes, por los subconjuntos de un conjunto determinado o por medidas de magnitud.
En este sentido, en lo que respecta a la relación entre diferentes conjuntos, es aquella en la que se estudian grupos con características diferentes, por ejemplo, la cantidad de medicamentos que necesita un determinado número de pacientes.
Por otro lado, la relación entre subconjuntos es la que se encuentra en un conjunto y los pequeños subconjuntos en los que se divide, un ejemplo de lo cual es la relación que existe entre el número total de pacientes de un hospital y los pacientes que pertenecen al área de cardiología del mismo.
Finalmente, las fracciones pueden representar relaciones entre diferentes medidas de magnitud; esto se observa fácilmente en las equivalencias entre kilogramos y libras, metros y pulgadas, millas y kilómetros, entre otras.
Tipos de fracciones
Los números fraccionarios son expresiones matemáticas compuestas por el numerador y el denominador, que dan como resultado la división de un todo en partes iguales. En este sentido, según el valor del denominador y el numerador, habrá diferentes tipos de fracciones, entre las que podemos mencionar
- Fracciones propias
Las fracciones propias son aquellas cuyo numerador tiene un valor inferior al denominador, es decir, el numerador es menor que el denominador. Ejemplos de este tipo de fracciones son: ½ (una mitad), 2/5 (dos quintos), 3/8 (tres octavos), entre otras. - Fracciones impropias
Por otra parte, las fracciones impropias son aquellas compuestas por un numerador superior al denominador; por lo tanto, son lo contrario de las fracciones propiamente dichas, y los siguientes son ejemplos de este tipo: 6/3 (seis tercios), 5/4 (cinco cuartos), 9/2 (nueve mitades), entre otros. - Fracciones unitarias
Otro tipo de fracciones, es el unitario; estas fracciones unitarias son aquellas cuyo numerador es igual a la unidad, es decir, el numerador es el número 1, mientras que el denominador está representado por cualquier otro entero positivo (mayor que 1). Ejemplo de las fracciones unitarias: ¼ (un cuarto), 1/9 (un noveno), 1/5 (un quinto). - Fracciones mixtas
Las fracciones mixtas combinan un entero con una fracción impropia como un todo; este tipo de fracción puede convertirse en fracciones impropias. Ejemplos de fracciones mixtas son 1 2/3 (un entero y dos tercios), 5 2/7 (cinco enteros y dos séptimos). - Fracciones equivalentes
Son fracciones equivalentes entre sí. Ese conjunto de fracciones cuyo resultado es el mismo, aunque sus numeradores y denominadores son diferentes. Por ejemplo, 3/6, 4/8 y 1/2 , las tres fracciones resultan en 0,5. - Fracciones decimales
Las fracciones decimales son aquellas en las que el denominador está representado por un número de potencia de diez (10, 100, 1000). Cabe señalar que las fracciones decimales también pueden expresarse como números decimales (con comas decimales), de ahí el nombre. Por ejemplo, 24/100 es una fracción decimal, que a su vez, puede escribirse como 0,24.