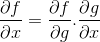
Funciones implícitas
Una correspondencia o una función se define implícitamente cuando la variable y no está clara, pero la relación entre x e y viene dada por una ecuación de dos incógnitas cuyo segundo miembro es cero.
Derivadas implícitas
La derivación implícita es una técnica que se aplica a las funciones definidas implícitamente, es decir, a las funciones definidas por una ecuación en la que el y no está claro. La ventaja de este método es que no requiere aclarar y encontrar la derivada.
Regla de la cadena
En la derivación implícita, siempre se respeta la regla de la cadena. Todas las expresiones diferenciales se darán según la variable independiente X. Así, cualquier variable θ diferente de X, debe incluir el término dθ/dx después de ser derivada.
Este término aparecerá sólo en primer grado o con un exponente igual a 1. Esta cualidad lo deja completamente claro bajo los métodos tradicionales de factorización. Por lo tanto, es posible obtener la expresión que define el diferencial dθ/dx.
La regla de la cadena muestra el carácter progresivo del proceso de diferenciación o de derivación. Donde para cualquier función compuesta f [ g(x) ], la expresión diferencial de f debe ser:
Aplicaciones de las derivadas implícitas
Los derivadas implícitas se utilizan en diversas situaciones. Son comunes en problemas de tipo de cambio entre variables relacionadas, donde, según el sentido del estudio, las variables se considerarán dependientes o independientes.
También tienen interesantes aplicaciones geométricas, como en los problemas de reflexión o de sombra, sobre figuras cuya forma puede ser modelada matemáticamente.
Se utilizan con frecuencia en las esferas de la economía y la ingeniería, así como en diversas investigaciones de fenómenos naturales y edificios experimentales.
Contenido