Representar gráficamente

Aunque hay diferentes maneras de representar las funciones matemáticas, debemos tener en cuenta que si hablamos de la misma función, no se alterará por mucho que cambie la forma en que se describe.

Representar gráficamente

Podemos definir una función y = f(x), como un criterio tal que a cada valor de la variable x le corresponde uno o más valores determinados de la variable y. No vamos a entrar en detalle en el tema de las funciones debido a su extensión, pero nos ceñiremos a su representación gráfica.

A través de la función y = f(x), tomaremos los diferentes valores de x como abscisas, y sus correspondientes valores de y como ordenados. De esta manera obtendremos una serie de puntos en el plano con los que, a través de su interpolación, haremos la gráfica de la función.

Veamos las diferentes gráficas que podemos obtener, según el tipo de función o ecuación aplicada.

Representación gráfica de una función lineal de primer grado

Sea la función lineal de primer grado: y = 3x.

Vamos a dar diferentes valores a x para hallar su correspondencia en y.

x = -2 ; y = -6

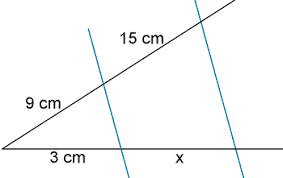
x = 0 ; y = 0 Vamos a representarla gráficamente.
x = 3 ; y = 9

Observamos que la recta de la función pasa por el origen de las coordenadas (0, 0). Esto es debido a que en este tipo de funciones en la que no existe término independiente, cuando la abscisa vale 0, la ordenada siempre valdrá 0.

Veamos ahora la función y = 2x + 3

x = -3 ; y = -3

x = 0 ; y = 3
x = 2 ; y = 7

En este caso la recta de la función no pasa por el origen de las coordenadas, sino que corta el eje de las ordenadas por el punto A (+3) y el eje de las abscisas por el punto B (-1,5). El punto A se obtiene cuando x = 0 y el punto B cuando y = 0.

Entrada Relacionada: Ejercicios de determinantes

y = 2 · (0) + 3 = 0 + 3 = 3 ; Coordenada (0, 3)

0 = 2x + 3

-2x = 3

2x = -3

x = -3/2 = -1,5 ; Coordenada (-1,5 , 0).

'OA' es el intercepto sobre el eje de las ordenadas (3), y 'OB' es el intercepto sobre el eje de las abscisas (-1,5). En este tipo de funciones el intercepto en el eje de las ordenadas es igual al término independiente (+3).

Representación gràfica de funciones de segundo grado

Sea la función:

Demos varios valores a x.

Veamos la gráfica.

Una vez que interpolamos los puntos obtenidos a través de la función, vemos que el gráfico representa una parábola ilimitada. Al ser una recta curva, el resultado será más preciso cuanto más puntos intermedios extraigamos de la función.

Como x está al cuadrado, ya sea su valor positivo o negativo, el resultado final para y será positivo e idéntico. Por ejemplo:

x = 2 ; y = 4

x = -2 ; y = 4

Veamos la función: