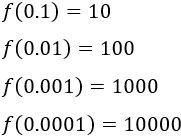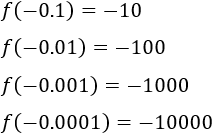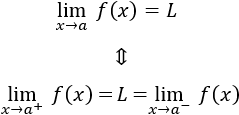¿Qué es el límite de una función?
El límite de una función es el valor al que tiende cuando la variable independiente tiende a un valor a (x → a) y se escribe:
Para ver el límite de una función en un punto, partimos del concepto de límite.
A cualquier punto a de la recta real (valor al que tiende x), podemos acercarnos, en el caso de la existencia del límite, tanto como queramos, por su izquierda como por su derecha. Estos son los límites laterales.
Al extremo derecho de la línea real, es decir, a +∞, sólo podemos acercarnos a ella desde la izquierda; al extremo izquierdo de la línea real, es decir, a -∞, sólo podemos acercarnos a ella desde la derecha. Ambos casos son los límites en el infinito.
En un punto de la variable x → a de una función f(x), podemos comprobar si el límite existe y su valor, dando valores a la variable cada vez más cerca de a, desde la izquierda y desde la derecha.
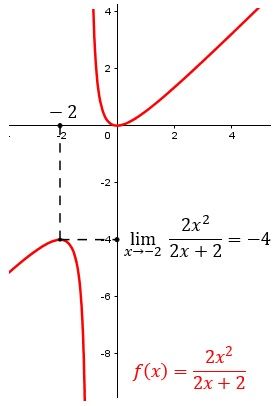
Veamos este límite:
Damos valores cada vez más cercanos a -2 en ambos lados, según esta tabla:
Como se ve en la gráfica:
No importa si f(x) está definido en a o no (en el ejemplo anterior, no está definido en x = -2) ni si el valor f(a) coincide con el límite. Lo que importa es el valor de la función cuando x se acerca cada vez más a a en su entorno.
Para calcular el límite de una función en un punto de su dominio, cuando son de tipo polinómico, racional, exponencial o logarítmico, o en las funciones trigonométricas restringidas de su dominio, basta con sustituir en x el valor a por el que queremos averiguar el límite.
Cómo resolver el límite de una función
Dejemos que sea una función y = f(x) , si queremos encontrar el límite de esa función en un determinado punto x = a, lo primero que haremos es encontrar f(a), ante el cual pueden darse tres casos:
- f(a) tiene un valor claro y unívoco.
- No podemos encontrar f(a) , ya sea porque f(x) no tiene imagen en el punto x = a, o porque nos da un valor indeterminado.
- f(a) nos da un valor infinito.
Para el primer caso, podemos decir que este mismo valor de f(a) es el valor límite en sí mismo. Esto ocurre en las regiones continuas de y = f(x) .
Por ejemplo:
Encuentra el límite en el punto x = 2 de la función y = x² +1
Este límite es 5, ya que de forma clara tenemos f(2) = 5.
Límites laterales
El límite de f(x) a la izquierda de a es L si la función toma valores cada vez más cercanos a L cuando x se aproxima al punto a la izquierda de la misma.
Lo denotaremos por:
De manera similar, el límite de f(x) a la derecha de a es L si la función toma valores cada vez más cercanos a L cuando x se aproxima al punto a la derecha de a.
Lo denotaremos por:
Ejemplo:
Consideremos la función f(x) = 1/x . Queremos calcular sus límites laterales en el punto x=0.
Cuando x toma valores cercanos a 0 a su derecha, f(x) toma grandes valores positivos:
Por lo tanto, su límite derecho es el infinito positivo:
el límite derecho de 0 de 1/x es +infinito
Cuando x toma valores cercanos a 0 a su izquierda, f(x) toma pequeños valores negativos:
Por lo tanto, su límite izquierdo es infinitamente negativo:
el límite derecho de 0 de 1/x es -infinito
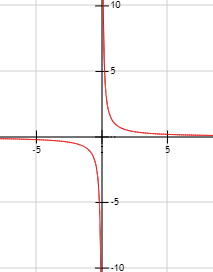
Gráfico de la función:
Lógicamente, hablamos del límite de una función en un punto en el que sus límites laterales coinciden:
Si no, decimos que el límite en a no existe. Esto es lo que sucede en el ejemplo anterior, así que:
Contenido