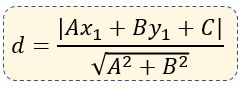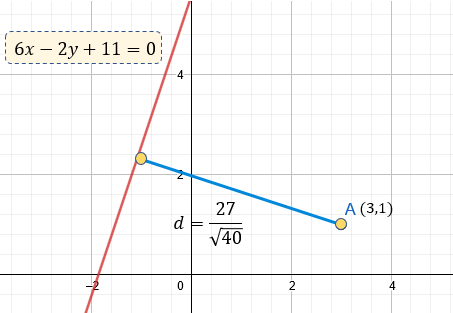
Distancia de un punto a una recta
La Distancia de un punto a una recta es una cuestión muy importante en la geometría analítica, ya que puede utilizarse en el cálculo diferencial e integral, y en la física. Por esta razón, analizaremos su fórmula:
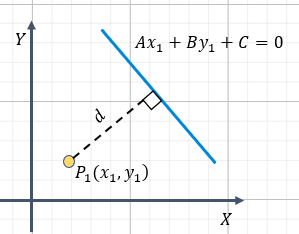
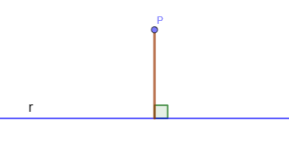
La fórmula se define para un gráfico similar al de la imagen:
Como vemos, lo que se calcula es la longitud del segmento perpendicular a la línea trazada desde el punto.
Veamos un ejemplo para comprender mucho mejor este asunto:
Encuentra la distancia del punto A (3,1) a la línea 6x -2y +11 = 0
Solución:
Para encontrar la distancia del punto A a la línea, sólo tenemos que sustituir nuestros datos en la fórmula, de la siguiente manera:
Sustituyendo las coordenadas del punto A y los coeficientes de la ecuación en la fórmula, obtendremos
Multiplicando el numerador, obtenemos
Ahora hacemos las operaciones en el denominador:
El valor absoluto de 27 es 27, entonces:
Entonces el resultado, es:
Un aproximado de 4.269 unidades, en una forma gráfica lo vemos así: