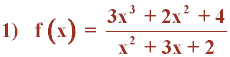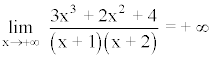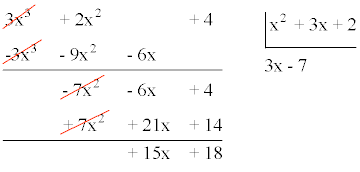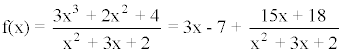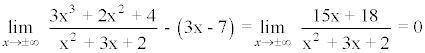Asíntotas verticales y horizontales
Como líneas rectas, la ecuación de una asíntota es simplemente la de una línea, y su expresión analítica dependerá de la elección del sistema de referencia (y = m-x + b en coordenadas cartesianas).
Aunque suelen representarse en el mismo sistema de coordenadas, las asíntotas no forman parte de la expresión analítica de la función, por lo que -en muchos ejemplos- no se incluyen explícitamente en el gráfico, o se indican mediante una línea punteada.
En muchos casos, las asíntotas coinciden con los ejes de coordenadas, es decir, sus ecuaciones en coordenadas cartesianas serán: x = 0, y = 0.
Hay tres tipos:
- Asíntotas verticales: líneas perpendiculares al eje de las abscisas, de la ecuación x = constante.
- Asíntotas horizontales: líneas perpendiculares al eje de las ordenadas, de la ecuación y = constante.
- Asíntotas oblicuas: si no son paralelas o perpendiculares a los ejes, de la ecuación y = m-x + b.
Ejercicios resueltos de asíntotas verticales y horizontales
Calcula las asíntotas de las siguiente función:
Asíntota vertical:
Las asíntotas verticales corresponden a los valores que anulan el denominador y no anulan el numerador. El denominador se puede descomponer de la siguiente manera:
x2 + 3x + 2 = (x + 1)(x + 2) ⇒ Las raíces son x = -1 y x = -2
Como ninguno de estos valores anula el numerador, ambos son asíntotas verticales.
Asíntota horizontal:
Para calcular las asíntotas horizontales calculamos el límite de la función al infinito.
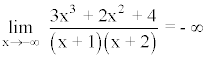
Por lo tanto, la función no tiene asíntotas horizontales.
Asíntota oblicua:
Realizamos la división de los polinomios:
Por lo tanto tenemos que:
Además se cumple lo siguiente:
Luego la recta y = 3x - 7 es asíntota oblicua de la función.
Contenido