Probabilidad condicional
La probabilidad condicional es la probabilidad de que ocurra un evento A, sabiendo que también ocurrirá otro evento B. La probabilidad condicional se escribe P(A|B) o P(A/B), y se lee "la probabilidad de A dada B".
No tiene por qué haber una relación causal o temporal entre A y B. A puede preceder a B en el tiempo, puede ocurrir o puede ocurrir simultáneamente. A puede causar a B, y viceversa, o puede no tener ninguna relación causal. Las relaciones causales o temporales son nociones que no pertenecen al ámbito de la probabilidad. Pueden desempeñar un papel o no, dependiendo de la interpretación que se dé a los acontecimientos.
Un ejemplo clásico es el lanzamiento de una moneda y luego el lanzamiento de un dado. ¿Cuál es la probabilidad de que el dado muestre un 6 si ya se ha tirado una cara de la moneda? Esta probabilidad se denota de esta manera: Q(6|C).
El condicionamiento de la probabilidad se puede lograr aplicando el teorema de Bayes.
Propiedades
-Toda probabilidad condicional está comprendida entre 0 y 1:
0 ≤ P (≤) ≤ 1
-La probabilidad de que el evento A ocurra, dado que dicho evento ocurre, evidentemente es 1:
P (A│A) = P (A∩A) / P(A) = P(A) /P(A) = 1
-Si los dos eventos son excluyentes, esto es, eventos que no pueden suceder simultáneamente, entonces la probabilidad condicional de que uno de ellos suceda es 0, ya que la intersección es nula:
P (A│B) = P (A∩B) / P(B) = 0 /P(B) = 0
-Si B es un subconjunto de A, entonces la probabilidad condicional también es 1:
P (B│A) = P (A∩B) / P(A) = 1
Importante
P (A│B) generalmente no es igual a P (B│A), por lo tanto hay que cuidar de no intercambiar los eventos al momento de encontrar la probabilidad condicional.
Probabilidad condicional ejemplos
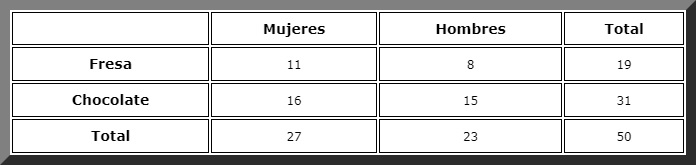
En una tienda de dulces se venden dos tipos de pasteles: de fresa y de chocolate. Al registrar las preferencias de 50 clientes de ambos sexos, se determinaron los siguientes valores:
-27 mujeres, 11 de las cuales prefieren el pastel de fresa y 16 el de chocolate.
-23 hombres: 15 prefieren chocolate y 8 fresa.
La probabilidad de que un cliente elija una tarta de chocolate puede determinarse aplicando la regla de Laplace, según la cual la probabilidad de cualquier evento es
P= número de eventos favorables/número total de eventos
En este caso, de 50 clientes, un total de 31 prefieren el chocolate, por lo que la probabilidad sería P = 31/50 = 0,62. Es decir, el 62% de los clientes prefieren la tarta de chocolate.
Pero, ¿haría alguna diferencia si el cliente es una mujer? Este es un caso de probabilidad condicional.
Tabla de contingencia
Luego se observan los casos favorables y se aplica la regla de Laplace, pero primero se definen los eventos:
-B es el evento "cliente femenino".
-A es el evento "preferir pastel de chocolate" siendo una mujer.
Vamos a la columna etiquetada como "mujeres" y allí vemos que el total es de 27.
Luego buscamos el caso favorable en la fila "chocolate". Hay 16 de estos eventos, así que la probabilidad que se busca es, directamente:
P (A│B) =16/27 = 0,5924
El 59,24% de las clientas prefieren el pastel de chocolate.
Este valor coincide cuando lo contrastamos con la definición inicialmente dada de probabilidad condicional:
P (A│B) = P (A│B) / P(B)
Aseguramos por la regla de Laplace y los valores de la tabla:
P(B) = 27 /50
P(A y B) = 16/50
Donde P(A y B) es la probabilidad de que el cliente prefiera el chocolate y sea mujer. Ahora los valores son sustituidos:
P (A│B) = P (A y B)/P(B) = (16/50) / (27/50) = 16/27=0,5924.
Y se verifica que el resultado es el mismo.
Contenido