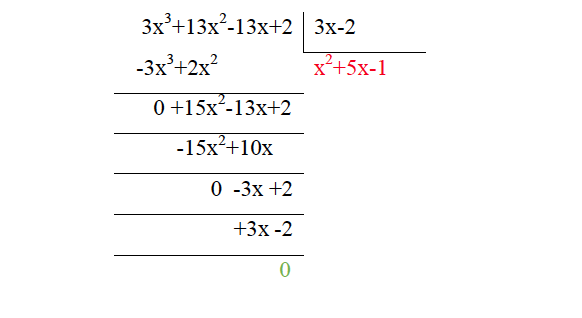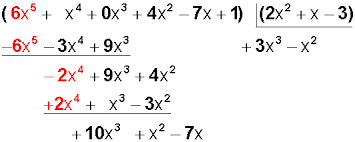
¿Qué es un polinomio?
Un polinomio es algo así como:
5xy+3x-1
Donde 5xy es uno de sus términos, 3x es otro término y -1 es el tercero de ellos.
¿Cómo se lleva a cabo la división de los polinomios?
División de monomios
Para dividir dos monomios debemos seguir los siguientes pasos:
(15x2) / (3x)=
- Divide los coeficientes. 15: 3=5
- Dividir la parte literal (las letras que aparecen en los monomios).
Así, (15x2) / (5x)= 3x
Ejemplos:
8 a / 2 a = (8/2).(a/a)= 4
15 ay /3a = (15/3) (a.y)/ a = 5 y
12 bxy / -2 bxy = (12/-2) (b.x.y)/(bxy.) = -6
-6 v2 . c. x/-3vc= (-6/-3) (v2 .c. x) /(v. c) = 2 v
División de un polinomio por un monomio
La división de un polinomio por un monomio (sólo si es posible) se obtiene dividiendo cada término del polinomio por el monomio, lo que da lugar a otro polinomio.
Ejemplo:
División entera de polinomios
Así, llamamos a la división exacta cuando R(x) es igual a 0. Para hacer la división debemos actuar de la misma manera que la división entera de los números naturales.
Vemos el siguiente ejemplo:
Sea:
P(x)= 3x3+13x2-13x+2
V(x)= 3x-2
Realice la siguiente operación:
(3x3+13x2-13x+2): (3x-2)=
Así: C(x)=x2-5x+1 y R(x)=0
Contenido